Diffraction grating problems

Hello! Thank you for your time and patience to have a look at my question!

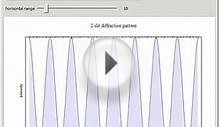
I am trying to simulate MEMS diffraction grating with COMSOL RF module and I have a problem with far-field domain calculation. The sensing scheme is attached here for your reference. The laser light source and photo detectors are placed 500um down under diffraction grating fingers(made of poly-silicon). Part of the light will be reflected by fingers and part will go through the slits between fingers and hit the gold mirror. The light reflected by mirrors and polisilicon fingers will have interference pattern in the far field. When the distance "g" between the mirror and fingers is changing, the diffraction pattern should also change.

My purpose is to calculate the light diffraction angle in far field. Based on this paper: (also attached here), I choose to use far-field domain to calculate the diffraction angle. When I was simulating one cell of the structure with periodic boundary condition, the result was fine. But when I try to simulate the real design our group fabricates, there are several problems.

1. The real structure has 51 fingers. I started with 11 fingers to see if far-field domain could work. But the far field pattern is almost indiscernible.

2. In my case with 51 fingers(with symmetry cut), I use background calculation and solve for scatter field. Based on Frauhofer diffraction theory, the light pattern will go to far field when d> 2*D^2/lamda (D:gating period lamda: wavelength d: distance between grating and observer In my case d>37.5um). Here I start far field integration at d=35um and do a parametric sweep to the distance "g" between mirror and fingers. However the case is too big for the server to solve.

My questions are:
1. Is there a more efficient way to calculate diffraction pattern? Far field calculation is too time consuming!!
2. In far field integration, does it matter if I start to integrate in a smaller domain(inside the near field)? How to choose the size of near field?

I have contacted COMSOL technical support twice and they suggested me to look at Plasmonic Wire Grating . But in this example, the wavenumber k of high order diffraction patterns are acquired analytically, it's more like "drawing" these patterns with COMSOL rather then solving them. In my case the wavenumber is still unknown so I did not use port boundary condition.