What is grating in Physics?

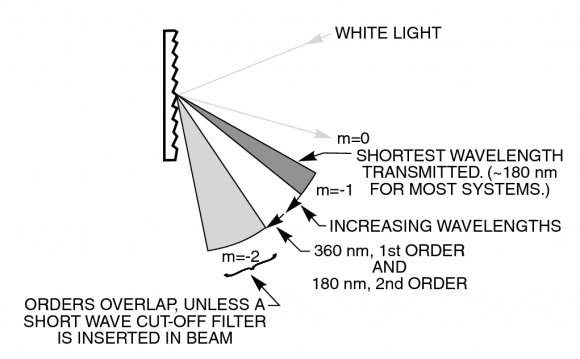
A monochromator, by definition, must separate the light into different wavelength beams.

Mirrors are only weakly wavelengthdependent, although some very sophisticated optical dielectric multilayers mirrors can have frequency dependence. Even so, the wavelength dependence of even a multilayer on direction is too weak for this application

Gratings on the other hand have a reflexion direction that is highly dependent on wavelength, given in the infinitely wide grating limit by the Bragg law. A finitely wide grating, comprising several thousand periods, approximates this closely. A grating system works like a phase antenna array with many periods. It is highly directional, and the direction dependence on wavelength is - within one order of the grating -locally monotonic. These properties make it ideal for wavelength tuning by altering its tilt relative to the beam.

The dependence is actually periodic and one gets many copies of the same spectrum output in different directions. The strength of each copy is set by the amplitude of the Fourier co-efficients describing the periodic spatial variation of the grating's surface. Thus a rectangular wave grating outputs odd-order copies of relative intensities $1, \, \frac{1}{3^2}\, \frac{1}{5^2}, \, \cdots$. However, within each copy, the scattering direction dependence on wavelength is monotonic.

User Sofia observes that one could in principle use a single slit or pinhole.

but why grating? Why not, just the double slit, or only 1 single slit? Technical problems?

This is right in principle. It's simply a question of frequency response, coupled power and mechanical tolerances. As you increase the number of slits, it's exactly like building up a phased array antenna from more and more elements. The system becomes more directional, and more frequency dependent (it's a simple Fourier transform relationship, the same kind that follows from $[\hat{x}, \hat{p}]=i\, \hbar\, \mathrm{id}$, so people often mistakenly call this phenomenon the photon uncertainty principle). Once you have more widely diffracted beams it makes the system cheaper and easier to build your tolerances can now be much coarser.

Further Comments

The OP asks

it is still unclear why the frequency separation via the phased array effect does not happen with a flat mirror, based on the Huygens principle.

A Huygen's principle view of this is that the relative phases of the Huygens transmitters are set by the incoming wave. If that wave is plane, you are correct, the Huygens transmitters do act as a phased array. That array's pointing direction is independent of wavelength and its scattered radiation plot is sharply peaked around the direction given by the reflexion law. Indeed, your understanding is exactly how one can explain the law of reflexion.

In contrast, a grating puts a phase modulation on these transmitters. For simplicity, let's assume there is a sinusoidal phase modulation. The scattered wave's direction will now be in the direction that annuls this phase modulation: with a sinusoidal modulation, there is indeed a direction where the optical path lengths of scattered light in that direction are all the same- it is as though the grating weren't there for light in this direction. That direction is given by the Bragg law. For all other scattering directions, the grating adds random phase to the wavefront and thus scattering in those directions is quelled by destructive interference.

The Bragg defined scattering direction is strongly wavelength dependent. I'd encourage you to draw a diagram of what I have said and do the phase calculations to see the difference between the two sitations.

I did miss the phase aspect, but now why would the grating per-se "fix" the "problem" of random phase? i.e. assuming the phase of the incident light is random, how does the grating make a coherent beam out of it?

Good question. Now we're getting into light's quantum nature. Let's say we're talking everyday light sources - something like a quartz halogen lamp used in the old monochromator light sources or even a laser - The crucial thing here is that they are not entangled. Now, in these cases, the photons are independent. In this kind of situation, the each photon interferes only with itself (to borrow Paul Dirac's famous, mostly true but not generally true phrase). So, what this means is that if you put your CCD or whatever at the output and turned the power down low so that only one photon is in the experimental kit at one time, then recorded where each hit the CCD, the pattern you would build up would be the same pattern as you would see if a powerful, continuously shining lightfield comprising zillions of photons reached the CCD.

Each photon by itself propagates following Maxwell's equations. So, if it comes from a long way off (from the quartz halogen filament) it will have a phasefont, exactly as does a classical Maxwellian wave. The overall phase of the photon field can is random, and the photon can be in a superposition of different frequencies (as it will be from an incandescent globe, although each photon still has a pretty narrow frequency range and the ensemble is broadened by the hot, thermalised source), so the Maxwellian structure - its wavefronts and all the rest, modulo the overall random global phase, is still there. The grating then imposes its phase modulation on this coherent object. You are to think of each photon like a little laser. So, if the source is a long way off, the grating is essentially processing plane waves, and the CCD elements in a detector will detect the photon with a probability proportional to the Maxwellian intensity. See my answer here for more details.

What won't work is if the source has a sizeable angular subtense relative to the input. What you then see is an image of the source with wildly coloured edges and smears, but the system won't work as a monochromator anymore. Monochromators have internal optics to make sure that the light striking the grating is as collimated as possible.