Wavelength of Laser light diffraction grating experiment

The diffraction grating was named by Fraunhofer in 1821, but was in use before 1800. There is a good case for describing it as the most important invention in the sciences.

Summary

• Demonstration: Looking through gratings (10 minutes)
• Discussion: Deriving the grating formula (20 minutes)
• Student experiment: Measuring wavelength (30 minutes)
• Student questions: Using the grating formula (30 minutes)
• Student experiment: A CD as a grating (home experiment) (30 minutes)
• Discussion: The meaning of coherence (10 minutes)

Demonstration: Looking through gratings
Pass around some diffraction gratings or hand-held spectroscopes. Invite students to look through them at various light sources: a torch bulb, LEDs of different colours, a sodium or mercury lamp. They should see a continuous spectrum (red to violet) for a white light source, but multiple images of different colours for coloured sources.

Shine a laser through a grating (as in the Young’s slits experiment above). Explain that light rays are emerging from each slit. What condition must be met for a maximum on the screen? (All rays must be in phase with each other.)

Observe the effect of moving the screen further away (the maxima are further apart). Try a grating with a different slit spacing. (Closer slits give maxima that are further apart.)

Shine a bright white light through the grating and observe the resulting spectra.

Describe the central maximum as ‘zero order’. The next maximum on either side is then ‘first order’ (n = 1), and so on. You will probably observe two or three on each side, far fewer than with a double slit. (It’s a much more demanding condition to have many rays in phase than just two.)

It is hard to overstate the importance of the diffraction grating to the progress of the sciences. Some would claim it as the most important invention, used in investigations from the structure of matter including DNA (being used as its own ‘grating’) to the structure of the Universe (from Doppler shifted spectral lines), and the determination of the composition of everything from stars to chemical compounds, by analysis of their spectra.

Discussion: Deriving the formula
You may need to derive (or simply present) the grating formulafirst derived by Young 1801:

d sin q = n λ

where d = the grating separation (the distance between slits). NB gratings are often specified as so many lines per metre (often on ‘old’ gratings as per inch, so beware if doing quantitative work!). Separations as small as 100 nm possible,

= 10 million lines per metre (equivalent to about 40, 000 lines per inch).

Note that this formula gives the directions for the maximum intensities (cf the single slit formula which gives directions for the minimum intensity).

Point out that smaller wavelengths give smaller angular separations. (You should have observed that violet light is diffracted less than red light.)

Student experiment: Measuring wavelength
Students can determine the wavelength of laser light using a diffraction grating. They could discuss the relative precision of this method, compared with the two-slit arrangement.

Student questions: Using the formula
Students can perform calculations relating to diffraction gratings.

They can interpret some images made using gratings.

Student experiment: A CD as a grating (home experiment)
Use a CD as a reflection diffraction grating. This experiment can be done at home.

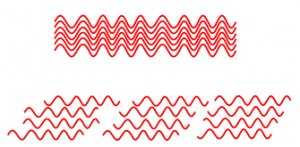
Discussion: The meaning of coherence
Now that your students have had practical experience of observing maxima and minima, further discussion of the necessary conditions should make sense. For superposition effects to be observable, the conditions must persist for a time long enough for them to be observed and extend far enough in space for a reasonably-sized pattern. It is easier for this to be the case if the waves have a well-defined frequency or wavelength (they must be monochromatic).

Ordinary light sources emit light in ‘overlapping bursts’, are not usually monochromatic (so the number of wavelengths in a given path can vary) and no source is a true point (so a range of path lengths is inevitably involved).

Laser light is particularly useful for showing interference effects because it is intense, highly monochromatic, and emitted in long wave trains and so maintains a constant phase relationship over large distances. We say that the waves arriving along two or more paths are said to be coherent.