Equation for diffraction

The intensity of the light in the diffraction pattern from a double slit is given by:

$$ I(\theta) = \cos^2\left(\frac{\pi d \sin\theta}{\lambda}\right) \tag{1} $$

We get maxima when the $\cos$ on the right side of the equation is $\pm 1$, and this happens when:

$$ \frac{\pi d \sin\theta}{\lambda} = \pi n $$

for the integer $n = 0, \pm 1, \pm 2$ and so on. A quick rearrangement gives the positions of the maxima as:

$$ \sin\theta = n \frac{\lambda}{d} $$

Which is where we get your expression for the spacing of the fringes. To see what happens as we decrease the slit spacing $d$ towards $\lambda$ let's use equation (1) to draw a graph of the intensity for various values of $d$:

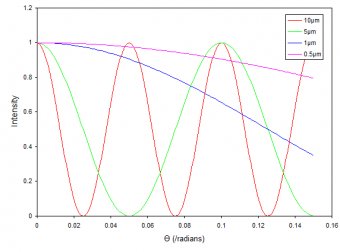
For this graph I've set $\lambda$ to 500nm and I've graphed the intensity for four values of $d$ from 10$\mu$m to 500nm. The graph shows that as we decrease $d$ towards $\lambda$ the spacing gets bigger and bigger until at $d = \lambda$ the spacing becomes so big that we only get one fringe. Remember that $\theta$ can't be less than $-\pi/2$ or greater than $\pi/2$ i.e. the maximum fringe spacing possible is $\pi$.

And that's why your equation does't have any solutions for $d < \lambda$. It's because the spacing betwen the fringes gets greater than $\pi$ and there is only one fringe.